Sebbene a questa domanda sia stata data una risposta, volevo solo aggiungere qualcosa per coloro che cercano una legge del potenziometro logaritmico ideale per la simulazione. Una mappatura dalla legge lineare alla legge logaritmica può essere trovata nella forma generale:

$$ y = a \ b ^ {x} + c $$

Lascia che questa funzione di equazione definisca una mappatura da \ $ 0 \ leq x \ leq1 \ $ a \ $ 0 \ leq y \ leq 1 \ $, dove \ $ a \ $, \ $ b \ $ e \ $ c \ $ sono parametri liberi per adattarsi alle curve desiderate.

Questa è un'equazione con tre parametri liberi, quindi possiamo scegliere tre vincoli per derivare i valori dei parametri. Per un potenziometro ideale, quando il tergicristallo è completamente al minimo, l'uscita non dovrebbe avere resistenza, quindi \ $ y = 0 \ $ quando \ $ x = 0 \ $, e così $$ 0 = a + c, \ quad c = -a $$ Quindi ora abbiamo l'equazione: $$ y = ab ^ x - a. $$ Il nostro secondo obiettivo è avere la massima resistenza quando il tergicristallo è completamente al massimo, cioè \ $ y = 1 \ $ quando \ $ x = 1 \ $, quindi $$ 1 = ab - a = a (b-1), \ quad a = \ frac {1} {b-1}. $$

Infine, possiamo scegliere un punto medio attraverso il quale vogliamo che la curva passi, che lascerò definibile dall'utente come \ $ y = y_m \ $ quando \ $ x = 0.5 \ $. Questo ci dà $$ y_m = a (\ sqrt {b} - 1) = \ frac {\ sqrt {b} - 1} {b - 1} = \ frac {1} {\ sqrt {b} +1} $$ e infine $$ b = \ left (\ frac {1} {y_m} - 1 \ right) ^ 2 $$

Questo ci fornisce una legge del potenziometro logaritmico parametrico che può cambiare la quantità di curva. Tieni presente che quando \ $ y_m = 0.5 \ $, \ $ a = \ infty \ $. Potresti fare una mappa lineare se scegli \ $ y_m = 0,5 - 10 ^ {- 5} \ $ o qualcosa del genere (ma perché dovresti!).

Di solito i taper pot audio non sono logaritmici ma un'approssimazione a tratti con solo 2 segmenti.

Ogni segmento del binario sarà rivestito con materiale di resistività diverso o avrà una larghezza diversa rispetto agli altri segmenti.

Ho visto vasi conici a filo avvolto in cui il primo ha una larghezza che cambia gradualmente per ottenere la pendenza variabile.

Un potenziometro lineare può essere utilizzato come cono logaritmico inserendo un resistore tra il tergicristallo e un terminale, come mostrato nel secondo diagramma ( Dalla guida di Elliot Sound Products ai potenziometri.)

Non esiste una formula per un vaso di log. Il meglio che puoi aspettarti è che la variazione di resistenza per angolo all'estremità "bassa" sia molto inferiore a quella all'estremità "alta". Sarebbe bello se fosse logaritmico, ma non lo è.

Come sottolinea la risposta di Kevin, l'approssimazione più comune è che la traccia abbia due diverse sezioni lineari (ish). È più economico da realizzare rispetto a una conicità variabile in modo continuo e più economico rispetto a 3 o più sezioni.

Sfortunatamente, la frase "log taper" ha più gradi di libertà oltre alla resistenza totale, è necessario anche il rapporto di sensibilità dall'alto verso il basso. Quindi, quando si acquista un potenziometro veramente logaritmico, dovrei specificare un potenziometro da "2 ottave" o da "3 ottave". I produttori e i distributori avrebbero bisogno di portare diversi tipi, vendendone di meno, quindi costando molto di più. Per un'applicazione audio, probabilmente non vorresti comunque il vero log, dovresti staccarti dal log a un livello basso e andare linearmente fino a zero.

Il motivo per cui non esiste una conicità logaritmica definita è che a nessuna base di clienti interessa esattamente quale sia la conicità da essere disposti a pagare abbastanza da far sì che i produttori si preoccupino di standardizzare qualcosa. I potenziometri vengono utilizzati principalmente nei dispositivi audio e, fintanto che la legge di rotazione è ragionevolmente "docile", a nessun cliente interessa davvero che il piatto fornisca (diciamo) 20 dB per 90 gradi, vogliono solo impostare un livello.

È interessante notare che la BBC ha affrontato questo problema nell'IIRC degli anni '50 / '60, quando volevano progettare nuove apparecchiature da studio e scoprirono che non potevano ottenere vasi di legno uguali da fonti diverse. Così hanno inventato un circuito pulito che utilizzava un potenziometro lineare per ottenere prestazioni logaritmiche, ma essendo un potenziometro lineare, era sempre riproducibile. Vedi se riesci a descrivere semplicemente come funziona e perché non scoppietta.

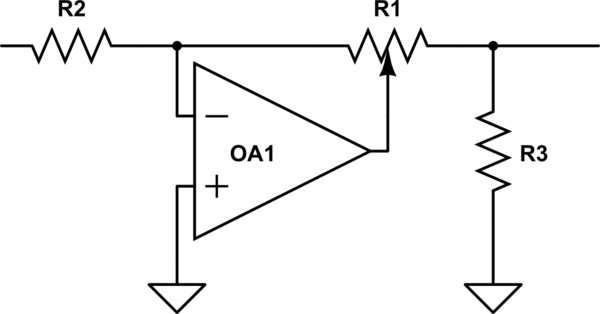
^{simula questo circuito. Schema creato utilizzando CircuitLab}

Se imposti un esperimento per misurare le leggi logaritmiche del tuo vaso, aspettati che la legge di un altro produttore sia diversa.

Questo schema utilizzato dalla BBC mi ha aiutato molto bene nella creazione di un log pot da un semplice lin pot nei miei progetti Arduino.Ho fatto i conti.Ecco i risultati:

Sia "a" l'impostazione del potenziometro (da 0 a 1)."H" è la funzione di trasferimento (implementata nel software, ovviamente).

H = a / (1 + (1 - a) * K)

Con K = 2 ciò fornisce un'approssimazione davvero piacevole di una funzione logaritmica, con un valore di 0,25 a 'a' = 0,5.

Per 0,1 (0,125, in realtà) come valore a metà strada, quanto segue funziona bene:

H = a * a / (1 + (1 - a) * K);con K = 2

Ho utilizzato un potenziometro digitale per agire come un semplice controllo del volume audio.Il segnale in entrata va a un'estremità della pentola, il segnale in uscita proviene dal tergicristallo e il terreno comune si trova all'altra estremità.Quindi se

M = Resistenza totale del potenziometro

R = Resistenza tra "volume zero" e tergicristallo

A = attenuazione richiesta in dB

Quindi questo sembra funzionare abbastanza bene:

$$ R = M \ 10 ^ {(A / 10)} $$

Come altri hanno già detto, l'estremità "zero" della corsa del piatto sarà di -∞ dB, quindi a un certo punto dovrai rinunciare alla riduzione lineare dei decibel.Ma al di sopra di quel punto di cutoff, potresti volere che i potenziometri equivalenti corrispondano a variazioni di decibel equivalenti - forse 5 gradi CCW taglia 1 dB.