Schema di esempio

Quindi per favore trova per il tuo divertimento, analisi del seguente circuito:

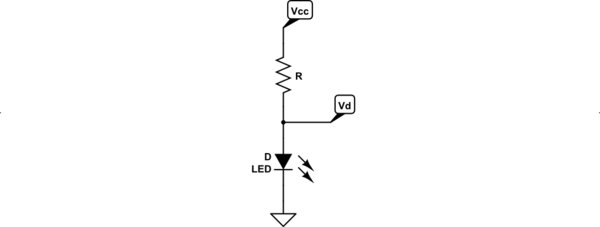
^{simula questo circuito - Schema creato utilizzando CircuitLab}

(La maggior parte del materiale che segue qui può essere facilmente trovata su questo sito Wikipedia: modellazione a diodi. Adotterò, tuttavia, un approccio diverso alla loro risposta a soluzione chiusa.)

Equazione del diodo di Shockley

Supponendo che funzioni alla sua temperatura di calibrazione, l'unica equazione rilevante per il LED è l'equazione del diodo Shockley:

$$ I_ \ text {D} = I_ \ text {SAT} \ left (e ^ {\ frac {V_ \ text {D}} {\ eta \, V_T }} - 1 \ destra) $$

Quell'equazione viene prontamente rielaborata per risolvere \ $ V_ \ text {D} \ $ :

$$ V_ \ text {D} = \ eta \, V_T \, \ operatorname {ln} \ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} + 1 \ right) $$

Quindi, abbiamo due diverse prospettive sul diodo / LED.

Per un BJT a segnale piccolo collegato a diodo, di solito accade che il coefficiente di emissione (noto anche come fattore di non idealità ) sia \ $ \ eta = 1 \ $ . Ma per molti diodi discreti come 1N4148 o 1N4007, \ $ \ eta>1 \ $ . (Non sarà inferiore a 1.) Alcuni LED avranno valori piuttosto alti (superiori a 4. non di rado.)

La corrente di saturazione, \ $ I_ \ text {SAT} \ $ , può essere vista meglio come un \ $ estrapolato y \ $ -axis intercetta. Ne parlo qui e anche qui e qui.

\ $ V_T = \ frac {k \, T} {q} \ $ è la tensione termica statistica ed è un parametro fisico di base con molti usi importanti. A temperatura ambiente, viene spesso considerato \ $ \ approx 26 \: \ text {mV} \ $ .

Soluzione matematica chiusa

L'equazione KVL per il circuito sopra è:

$$ \ begin {align *} V_ \ text {CC} - R \, I_ \ text {D} - V_ \ text {D} & = 0 \: \ text {V} \\\\ V_ \ text {CC} - R \, I_ \ text {D} - \ eta \; V_T \, \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right )} & = 0 \: \ text {V} \ end {align *} $$

Il problema qui è risolvere per \ $ I_ \ text {D} \ $ . Puoi facilmente risolverlo in modo iterativo. Oppure, se hai un pezzo di carta con l'equazione del diodo tracciata, puoi usare un righello per aggiungere la "linea di carico" del resistore e trovare un'intercetta approssimativa. Ma per una soluzione matematica chiusa senza iterazione, è necessaria la funzione di log del prodotto (nota anche come funzione LambertW):

$$ \ begin {align *} V_ \ text {CC} - R \, I_ \ text {D} - \ eta \; V_T \, \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right )} & = 0 \: \ text {V} \\\\ \ frac {V_ \ text {CC}} {\ eta \, V_T} - \ frac {R \, I_ \ text {D}} {\ eta \, V_T} & = \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right)} \\\\ e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T} - \ frac {R \, I_ \ text {D}} {\ eta \; V_T}}} & = \ frac { I_ \ text {D}} {I_ \ text {SAT}} \\\\ 1 & = \ frac {I_ \ text {D}} {I_ \ text {SAT}} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T} - \ frac {V_ \ text {CC}} {\ eta \, V_T}}} \\\\ e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} & = \ frac {I_ \ text {D}} {I_ \ text {SAT}} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T}}} \\\\ \ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} & = \ frac {R \, I_ \ text {D}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T}}} \\\ \ & \ text {set} u = \ frac {R \, I_ \ text {D}} {\ eta \, V_T} \\\\ & \ quindi \\\\ u \, e ^ u& = \ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T }}} \\\\ u& = \ operatorname {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \\\\ \ frac {R \, I_ \ text {D}} {\ eta \, V_T} & = \ operatorname {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \\\\ I_ \ text {D} & = \ frac {\ eta \, V_T} {R} \ cdot \ operatorname {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \ end {align *} $$

(Per chi è interessato a maggiori dettagli sulla funzione di registro del prodotto, nota anche come LambertW, consultare il sito LambertW di Wolfram.)

Ora, supponiamo che \ $ V_ \ text {CC} = 9 \: \ text {V} \ $ e \ $ R = 220 \: \ Omega \ $ . Per il LED, utilizziamo i parametri presi da un LED Luminus PT-121-B: \ $ \ eta = 8.37 \ $ e \ $ I_ \ text {SAT} = 435.2 \: \ text {nA} \ $ . (Supponiamo \ $ V_T \ approx 26 \: \ text {mV} \ $ , ovviamente.) Quindi troveremmo \ $ I_ \ text {D} \ approx 29.9 \: \ text {mA} \ $ e \ $ V_ \ text {D} \ approx 2.42 \: \ testo {V} \ $ . Questo è molto vicino alla simulazione Spice per il dispositivo e le circostanze.

Oppure supponiamo di utilizzare i parametri per 1N4148, \ $ \ eta = 1.752 \ $ e \ $ I_ \ text {SAT} = 2.53 \: \ text {nA} \ $ e usa \ $ V_ \ text {CC} = 5 \: \ text {V} \ $ e \ $ R = 1 \: \ text {k} \ Omega \ $ . Quindi, per questo diodo comune, troveremmo \ $ I_ \ text {D} \ approx 4.34 \: \ text {mA} \ $ e \ $ V_ \ text {D} \ approx 654 \: \ text {mV} \ $ .

Come puoi vedere, funziona per tutti i tipi di diodi. (Il limite principale è il fatto che \ $ I_ \ text {SAT} \ $ varia ampiamente rispetto alla temperatura - discusso verso la fine della discussione su ' modelli a diodi semplificati ", dove vengono ulteriormente discusse le sue variazioni dovute a uno dei risultati più importanti della meccanica statistica, il fattore Boltzmann.)

Riepilogo

Le soluzioni chiuse per domande di base sui diodi non sono mai basilari. Tuttavia, per la maggior parte degli scopi di solito è sufficiente fare alcune ipotesi semplificative ed essere "abbastanza vicini a tutti gli effetti". (Per leggere su alcuni di questi, vedere "modelli a diodi semplificati" già menzionati un attimo fa.) Quindi probabilmente non avrai mai bisogno di fare il lavoro di cui sopra. È semplicemente bello sapere cosa è coinvolto, se te lo chiedi. (Per lo più, quindi ti renderai conto del motivo per cui usi questi presupposti semplificatori, invece.)

Tieni anche presente che la soluzione chiusa è una soluzione su larga scala e risolve la domanda in una gamma molto, molto ampia di circostanze.

Ti stavi chiedendo cosa succede quando la tensione applicata è uguale alla tensione del diodo. Ma, in realtà, la tensione del diodo si adatta alle circostanze. Non è risolto. Quindi se provi ad applicare la cosiddetta "tensione del diodo" al circuito, il diodo regolerà invece la sua tensione ancora più in basso in modo che la caduta di tensione del resistore sia "appena sufficiente" per fornire la corrente che è "appena fornire la tensione del diodo necessaria per compensare la differenza. Questa è la vera risposta qui. La soluzione matematica di cui sopra è solo un modo complicato per dire la stessa cosa, ma quantitativamente invece che in modo "ondeggiante".

Tutto quanto sopra si applica esattamente come per qualsiasi diodo a polarizzazione diretta di qualsiasi tipo. Anche quelli con una sostanziale resistenza ohmica (nell'applicazione) (che viene poi aggiunta alla resistenza in serie per l'analisi).

Se hai un grafico della corrente rispetto alla tensione per un diodo, puoi disegnare delle "linee di carico" su di essi per risolvere la tua domanda. Eccone uno che avevo creato per i LED alimentati da un'alimentazione a 5 V. Le tensioni sono superiori a quelle di un normale diodo ma il principio è lo stesso.

Figura 1. Il circuito semplice.

Figura 2. Corrente rispetto alla tensione diretta per una gamma di LED di diversi colori con linee di carico per vari valori di resistenza. Fonte: strumento grafico di resistenza della linea di carico.

Se prendiamo il caso da 100 Ω della Figura 2 e il LED UV (perché è il più vicino alla tensione di alimentazione di 5 V) possiamo fare le seguenti osservazioni:

• Se V _f è 0 V, ci sono 5 V su R1 e la corrente sarebbe 5/100 = 50 mA. La linea di carico di 100 Ω inizia da (0, 50).
• Se V _f è 5 V allora c'è 0 V su R1 e la corrente sarebbe 0 mA. La linea di carico di 100 Ω termina a (5, 0).
• Per vedere quale corrente scorre attraverso il LED UV su un'alimentazione a 5 V con 100 Ω per R1, basta trovare l'intersezione della linea di carico con la curva UV. Questo è a 3,5 V e 15 mA.
• Dato il valore del resistore o la corrente desiderata, puoi stimare rapidamente l'altro dal grafico.

Quindi, torniamo alla tua domanda:

Se un diodo è in serie con un resistore e una sorgente di tensione impostata sul valore esatto della caduta di tensione diretta del diodo, quale sarà la caduta di tensione attraverso il resistore?

Si spera che ora sia chiaro che un diodo non ha una caduta di tensione diretta "esatta".

Non può essere zero ma immagino che debba essere vicino. Abbiamo imparato che normalmente sottraresti la tensione diretta (0,7 V) dal circuito, ma questa circostanza non ha senso per me.

La tua intuizione è corretta. Devi solo ricordare che il grafico corrente rispetto a V _f è una curva, non un angolo retto.

Il diodo è un elemento non lineare.Per la tua domanda, assuming un diodo ideale:

1. Il diodo quando polarizzato in avanti inizia a condurre completamente a 0,7 V.

2. Anche la sorgente di tensione è impostata con precisione a 0,7 V.

3. La caduta di tensione attraverso la R appare quando c'è un flusso di corrente.La corrente non può fluire poiché non c'è differenza di tensione attraverso il resistore.Drop è zero attraverso il resistore.

Assumi una sorgente di tensione ideale e una resistenza zero per il resistore.

• La corrente sarà zero se la tensione è inferiore o uguale a 0,7 V.
• La corrente sarà infinite se la tensione è maggiore di 0,7 V.

Il problema qui è che OP pensa che la caduta di tensione attraverso il diodo sia VF (circa 0,7 V); quindi, includendo una sorgente di tensione con la stessa tensione VF, il risultato dovrebbe essere zero. Tuttavia, questo è valido se una corrente sufficiente scorre attraverso il diodo (ad esempio, è un requisito di base per uno stabilizzatore di tensione Zener) ... e ciò richiede una tensione di alimentazione più elevata, che in questo caso non è da nessuna parte. Di conseguenza, come dicono i professionisti, "il diodo non è adeguatamente polarizzato". Ho illustrato graficamente questa situazione in Fig.1. Esaminiamolo.

Fig. 1. Per funzionare correttamente nella parte verticale della sua curva IV, il diodo deve essere adeguatamente polarizzato

Per funzionare correttamente (nella parte quasi verticale della sua curva IV), il diodo richiede una corrente più significativa (IB) che può essere ottenuta da una tensione più alta V e dalla resistenza R. Di conseguenza, la linea di carico (in marrone ) interseca la curva IV del diodo al centro della parte verticale - il cosiddetto "punto operativo" B, e la caduta di tensione attraverso il diodo è VF = 0,7 V.

Tuttavia, la tensione di ingresso dell'OP è solo VF. Quindi la linea di carico si è significativamente spostata a sinistra ... e ora interseca la curva IV del diodo nella parte (quasi) orizzontale della curva IV - punto A (il punto di lavoro si è spostato dalla posizione B alla posizione A). Ora la corrente IA è insufficiente ... e la caduta di tensione sul diodo è inferiore a VF.

Quindi, formulata in questo modo, la domanda non ha valore pratico. È solo una situazione indesiderata nelle applicazioni con diodi analogici. Ma se in qualche modo il diodo è adeguatamente polarizzato, la domanda degli OP ha senso e può illustrare molte applicazioni interessanti e importanti.

"Biasing" significa semplicemente "aggiungere" una tensione costante alla tensione di ingresso esistente (V + nella figura). Se non ci fosse un terreno, ci sarebbe un solo modo per farlo. Ma poiché di solito mettiamo a terra il diodo (come nella figura), possiamo farlo in due modi possibili: dal lato dell'anodo ("tirandolo" verso l'alto) e dal lato del catodo ("tirandolo" verso il basso). Consideriamo quest'ultimo come più interessante e più facilmente implementabile - Fig. 2.

Fig. 2. Polarizzazione di un diodo dal lato del catodo

Per polarizzare il diodo, abbiamo collegato un'altra (ma negativa) sorgente di tensione V-. Come possiamo vedere dall'immagine della tensione (barre rosse), possiamo regolare V + per renderlo uguale a VF del punto di lavoro C (al centro della parte verticale). Di conseguenza, la tensione di "uscita" (del catodo) è zero (la cosiddetta "massa virtuale"). Come se la tensione V + avesse neutralizzato la caduta di tensione VF attraverso il diodo ... e la tensione totale di questa rete composta da V + e D fosse zero. In senso figurato, possiamo pensare alla rete come a un "diodo ideale" con caduta di tensione zero VF. Inoltre, con più immaginazione, possiamo considerare la sorgente di tensione V + come una sorta di "diodo negativo" -D che rimuove il "diodo positivo" D. È negativo poiché aggiunge tensione mentre il diodo ordinario è positivo poiché sottrae tensione.

Il nome di questa tecnica (può essere) "compensazione di tensione" ... dove compensiamo una caduta di tensione indesiderata con una tensione equivalente in modo serie. Può essere passivo se la FV viene compensata da un'altra FV su un diodo uguale. Questa tecnica è ampiamente utilizzata per polarizzare gli stadi complementari di uscita (op) amp con reti di diodi e "diodi attivi" collegati tra basi di transistor. Un'altra applicazione può essere trovata in H&H AE (pagina 52, Fig. 1.93) dove un convertitore log a diodi viene compensato in questo modo.

Tuttavia, molto più interessante è la compensazione della tensione attiva . Possiamo vederlo nel circuito di un convertitore log dell'amplificatore operazionale se lo disegniamo in un modo più insolito - Fig. 3. Gli elementi con tensioni positive sono disegnati sopra la linea di tensione zero (massa) ; gli elementi con tensioni negative sono disegnati sotto la linea di tensione zero.

Fig. 3. Nel convertitore log dell'amplificatore operazionale, l'amplificatore operazionale compensa VF aggiungendo la stessa tensione -VF

L'amplificatore operazionale funge da sorgente di tensione variabile V + dalla Fig. 2 sopra. "Va" sotto lo zero per aggiungere la tensione VF in serie al diodo. Di conseguenza, la tensione di "uscita" dell'anodo è zero ( massa virtuale ) ... l'amplificatore operazionale ha neutralizzato la caduta di tensione VF attraverso il diodo ... In senso figurato, possiamo pensare della combinazione di amplificatore operazionale (adeguatamente fornito), alimentazione V- e diodo imperfetto come di un "diodo ideale" con caduta di tensione zero VF ... o, come sopra, possiamo pensare all'amplificatore operazionale come una specie di "diodo negativo" -D che rimuove il "diodo positivo" D ...

La caduta di tensione su un diodo (reale) non è fissa, ma varia in base alla corrente, alla temperatura e forse ad altre condizioni.

Mentre nel tuo circuito aumenti lentamente la tensione della sorgente, aumenterà anche la caduta di tensione sul diodo: non sarà mai maggiore della sorgente (altrimenti hai un generatore, non un diodo).Quindi scorre una corrente, il resistore abbassa un po 'di tensione e il sistema trova (automaticamente) un equilibrio perché con meno corrente e tensione, il diodo abbassa la sua caduta di tensione.

Penso che ci sia una risposta "Elettronica 1" molto più semplice alla tua domanda.

La tensione attraverso il diodo e la tensione attraverso il resistore devono sommarsi a quella della sorgente di tensione.Quindi, se la caduta di tensione attraverso il diodo è la sua caduta di tensione diretta (che sarebbe il caso in un semplice modello di diodo ideale - e questa è la semplificazione che ti sto suggerendo di fare), allora la caduta di tensione attraverso il resistore è zero.Un corollario è che non scorre corrente.

Diverse altre risposte ti diranno perché questa semplificazione non è sempre accurata, ma dato che non hai fornito altri dati sul diodo (presumibilmente perché te ne è stato dato uno), ti suggerirei di farela semplificazione di cui sopra.

Esiste un grafico tensione vs corrente per il diodo.Ipotizzando una tensione e un livello di corrente specifici sul grafico si può determinare che una variazione infinitesimale di tensione e corrente rappresenta una resistenza equivalente, quindi in serie con il resistore limitatore di corrente.Puoi anche stimare la tensione del led, presumere la corrente di tensione e la potenza attraverso il resistore in base a Vcc meno questa tensione, cercare la tensione sul grafico a questa corrente e regolare le stime di corrente in base a questa Vcc rivista meno questo valore di tensione di giunzione regolato di conseguenza.Tieni presente che a causa dell'aumento della tensione di giunzione a causa della temperatura, sarai approssimativo.