Se si dispone di uno schema esistente costituito da inverter, AND e OR Gate, è disponibile un semplice processo in tre fasi che è possibile seguire per convertire il circuito in tutte le NAND (è possibile modificare leggermente il processo per NOR). Puoi usare "Bubble Logic".

Supponiamo che tu abbia tre livelli di logica. Il primo livello, più vicino ai tuoi input, è costituito dagli inverter. Il secondo livello è costituito da porte AND. E il livello finale consiste in un solo cancello OR. Alcuni libri di testo possono riferirsi a questa come un'espressione di "somma di prodotti" algebra booleana.

1. Converti tutte le tue porte AND in porte NAND.
2. Ovunque hai aggiunto una bolla , hai effettivamente invertito la funzione di algebra booleana su quel filo. Quindi, aggiungi un'altra bolla a quel filo e disegna la bolla vicino alla porta OR sull'uscita.
3. Una porta NAND è equivalente a una porta OR i cui ingressi sono invertiti. Quindi, se la porta OR all'uscita ha tutti i suoi ingressi invertiti, ridisegnala semplicemente come una porta NAND. Se non lo fa, fallo aggiungendo una bolla vicino all'ingresso in sala operatoria e un'altra bolla (inverter) da qualche altra parte su quel particolare cavo.

Potresti eseguire un un'implementazione del tutto NOR. Spero che questo aiuti!

Basandosi sulla risposta di Bob e sulla tua domanda sulle equazioni: il concetto di base da ricordare è il teorema di DeMorgen. Usando + per OR, * per AND e ~ per NOT,

~ (a + b) = (~ a * ~ b)

~ (a * b) = ( ~ a + ~ b)

In altre parole, l'uscita di una porta NOR è equivalente all'uscita di una porta AND con gli ingressi invertiti. E, viceversa: l'output di una porta NAND è equivalente all'output di una porta OR con gli ingressi invertiti.

Se sposti le inversioni tutte da un lato ottieni:

(a + b) = ~ (~ a * ~ b)

(a * b) = ~ (~ a + ~ b)

In altre parole, una porta OR è equivalente a una porta NAND con ingressi invertiti e una porta AND è equivalente a una porta OR con ingressi invertiti.

Il trucco da realizzare è che puoi spostare le "bolle" e implementare il teorema di DeMorgen con lo schema. Ho sentito questo chiamato "il gioco delle bolle". L'idea è di capire quale funzione ti serve con solo "logica positiva" usando AND e OR. Quindi gioca al gioco delle bolle e crea tutte le NAND e NOR con le bolle sugli ingressi, quindi sposta le bolle lungo le linee (due su una linea si annullano) per creare semplici NAND e NOR. A volte è necessario anche un inverter aggiuntivo qua o là.

Il gioco delle bolle ha quattro regole:
1) Puoi cambiare AND o OR in (N) AND e (N) OR con bolle su tutti i terminali.2) Puoi "spingere" una bolla dall'output indietro agli input, rendendoli tutti invertiti.3) Puoi "spingere" le bolle da tutti gli input fino all'output, invertendo l'output.4) Due bolle su una riga si annullano.

Ecco un esempio.

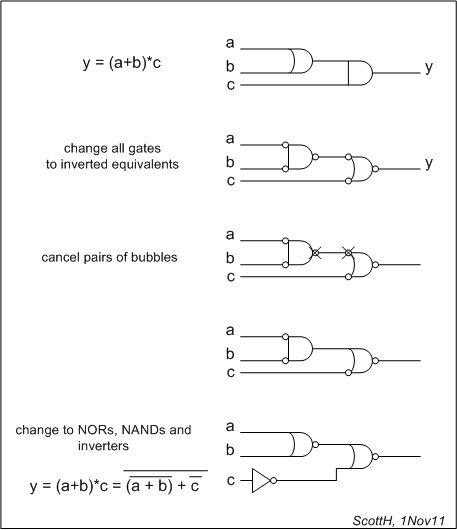
Si scopre che se cambiamo solo il gate di output possiamo salvare un passaggio o due ...

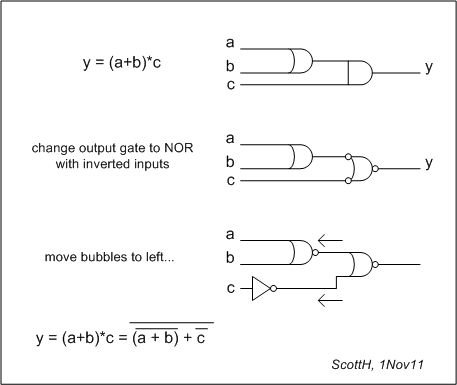
Saluti.

• PER DUE PORTE DI INGRESSO:

  Ingressi = A, B

  "+" = OR

  "." = AND

AND

• OUTPUT è vero se A AND B è vero,
  Altrimenti non vero

  Risultato vero se sia A E B sono entrambi veri.

  • X = AB

OR

• L'output è vero se A OR B è vero,
  Altrimenti non vero

  Restituisce vero se A è vero OR se B è vero O se entrambi sono veri.

  • X = A + B

XOR

• L'output è vero se A è esclusivamente vero OPPURE se B è esclusivamente vero.
  Altrimenti falso.

  • X = A./B + / AB
    (Output = A e non B o B e non A.

NAND - l'uscita è invertita da AND
NOR l'uscita è invertita da OPPURE
XOR lascia abbastanza bene da solo.

PER GATES N-INPUT

E

• OUTPUT è vero se A AND B AND C AND ... è vero,
  altrimenti non è vero. TUTTI deve essere vero affinché l'output sia vero

OR

• L'output è vero se A OR B OR C OR ... è vero,
  altrimenti non è vero

  QUALUNQUE o più può essere vero & almeno uno deve essere vero affinché l'output sia vero

XOR

• L'output è vero se uno qualsiasi di ABCDR ... è esclusivamente vero OPPURE se B è esclusivamente vero. Altrimenti falso.

THEN:

NAND = NOT AND l'output è invertito da AND
NOR - NOT OR l'uscita è invertita da OPPURE
XOR lascia stare abbastanza bene :-)

Quella pagina sembra mostrare tabelle di verità per le funzioni logiche di base. Queste sono cose che devi solo sapere.

Fortunatamente, non è poi così misterioso o difficile. AND e OR fanno solo quello che dicono. Per una porta AND, l'ingresso A AND l'ingresso B deve essere vero (alto logico) affinché l'uscita sia vero (alto logico). Per una porta OR, l'ingresso A OR l'ingresso B deve essere vero affinché l'output sia vero. Sì, è davvero così semplice. Ancora una volta NAND è ciò che dice, che è NON-AND. L'output di una NAND è l'opposto (NOT) di un AND. NÉ è NOT-OR. L'output è l'opposto dell'output di un gate OR.

Questo è tutto molto semplice. È come dover imparare che 3 più 2 fa 5 prima di poter eseguire operazioni aritmetiche più complicate.

Ricorda solo l'aggiunta per OR
e la moltiplicazione per AND Gates, quindi
Se moltiplichi un numero qualsiasi per 0, otterrai 0 quello che potrebbe essere l'altro
input, quindi inverti il ​​risultato come come
"Se ottieni 0 rendilo 1 o se ottieni 1 rendilo 0 per ottenere le uscite della porta NAND"
Come quello
quando aggiungi un numero qualsiasi a 1, l'output è 1 (alto ) quale potrebbe essere l'altro input, quindi invertire nuovamente il risultato ottenuto e quello sarà l'output per il gate NOR.

Per evitare confusione, ricorda solo l'aggiunta per OR e la moltiplicazione per AND
è così che puoi andare facilmente.